2023美赛A题代码

埋葬自己

来历：知乎



2023.2.18：更新微分方程求解代码
已更新2023美赛A题1-6问具体模子公式和代码，建立最优物种合作微分方程模子，思绪、模子方程公式和代码具体内容见文末。2023美赛A题翻译以下：
分歧品种的动物对压力的反应方式分歧。例如，草原对干旱很是敏感。干旱以分歧的频次和分歧的严重水平发生。大量的观察表白，分歧物种的数目对动物群落在履历了持续几代的干旱循环时若何顺应起到了感化。在一些只要一种动物的群落中，下一代对干旱条件的顺应才能不如具有四种或更多物种的群落中的个体动物。这些观察成果提出了很多题目。例如，动物群落从这类当地化的生物多样性中受益所需的最低物种数目是几多？随着物种数目的增加，这类现象是若何扩大的？这对动物群落的持久保存才能意味着什么？
斟酌到干旱顺应性与动物群落中物种数目的关系，你的使命是摸索和更好地了解这一现象。具体地说，你应当：
[1] 开辟一个数学模子来猜测动物群落在表露于各类不纪律的天气周期时若何随着时候的推移而变化。包括应当有充沛降水的干旱期间。该模子应当斟酌到干旱周期平分歧物种之间的相互感化。
摸索关于动物群落和更大情况的持久相互感化，您可以从您的模子中得出什么结论。斟酌以下题目
[2] 需要几多分歧的动物物种才能使群落受益，随着物种数目的增加会发生什么？
[3] 群落中的物品种型对你的成果有什么影响？
[4] 在未来的天气周期中，干旱发生的更频仍和更普遍的变化会发生什么影响？假如干旱不那末频仍，物种的数目对整体群落能否有一样的影响？
[5] 净化和栖息地削减等其他身分对你的结论有什么影响？
[6] 你的模子表白应当做什么来确保动物群落的持久保存才能，对更大的情况有什么影响？
您的PDF处理计划的总页数不应跨越25页，应包括：
单页摘要表。
目录。
为您供给完整的处理计划。
参考列表。
注：MCM大赛以25页为限。您提交的一切方面都计入25页的限制(摘要表、目录、报告、参考列表和任何附录)。你必须援用你的想法、图片和报告中利用的任何其他材料的来历。
生物多样性：天下上或特定栖息地或生态系统中的生物多样性。
下面是思绪和具体的模子展现：
1.1 建立一个数学模子，猜测一个动物群落在各类不法则的天气周期中若何随时候变化。包括本该降水充沛的干旱期间。该模子应斟酌到干旱周期平分歧物种之间的相互感化。

看到群落一词，我们建立物种合作模子，并加入情况身分（降水量）
首先简单起见，先建立2生物，无情况身分的合作模子：
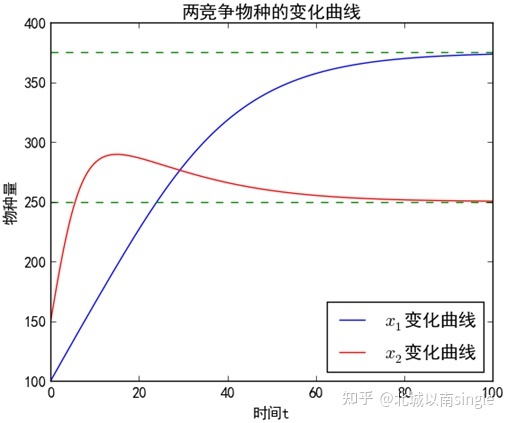
研讨在同一个自然情况中保存的两个种群之间的合作关系。假定两个种群独安闲这个自然情况中保存时数目演变都服从Logistic纪律，又假定当它们相互合作时城市减慢对方数目的增加，增加速度的减小都与它们数目的乘积成反比。依照这样的假定建立的常微分方程模子为
\left\{ \begin{array}{l}         \frac{dx_1}{dt}=r_1x_1\left( 1-\frac{x_1}{N_1} \right) -a_1x_1x_2\\         \frac{dx_2}{dt}=r_2x_2\left( 1-\frac{x_2}{N_2} \right) -a_2x_1x_2\\ \end{array} \right.  
方程的另一种形式为：
\left\{ \begin{array}{l}         \frac{dx_1}{dt}=r_1x_1\left( 1-\frac{x_1}{N_1}-\alpha \frac{x_2}{N_2} \right)\\         \frac{dx_2}{dt}=r_2x_2\left( 1-\frac{x_2}{N_2}-\beta \frac{x_1}{N_1} \right)\\ \end{array} \right.  
其中r为增加率，N为物种最大容量，
α：物种2对物种1的合作系数，即每个N2个体所占用的空间相当于α个N1个体所占用空间。
β：物种1对物种2的合作系数，即每个N1个体所占用的空间相当于β个N2个体所占用空间。
设备求解参数，参数与代码见文末[1]
这些参数表白，  x_1  是一个增加相对缓慢的物种，可是种内合作较小，而且不轻易遭到  x_2 物种的影响，是以，久远来看， x_1 物种将在该自然情况中占优；相比之下， x_2 物种的增加速度较快，可是种内合作较大，而且轻易遭到 x_1 物种的影响，部分代码以下：
from scipy.integrate import odeint
import numpy as np
from scipy.optimize import leastsq
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei'] #这两句用来一般显现中文标签
plt.rcParams['axes.unicode_minus'] = False

t = np.arange(0,100,0.1)

def deriv(w,t,a,b,c,d,e,f):
    x,y = w
    return np.array([ a*(1-b*x)*x-c*y*x, d*(1-e*y)*y-f*x*y])

现在将模子扩大一下，建立多物种合作模子，也就是群落的合作模子，
将公式2扩大一下，公式见文末文档
其中ri为增加率，Ni为物种最大容量， \alpha_i :物种k对物种i的合作系数，即每个Nk个体所占用的空间相当于
个Ni个体所占用空间。
然后我们再加入加入情况身分（降水量）的影响
我们晓得，降水量（标记h暗示降水量）应当首要影响的是发展率，所以首要使命是建立以降水量h为自变量，发展率为因变量的函数。
以降水量h为自变量，发展率为因变量的函数能够是以下形式：
[1] 发展率与降水量h成反比
r_i\left( t \right) =k*h\left( t \right)  
[2] 发展率与降水量h成logistic关系，这一关系的缘由简单诠释一下：降水量多的时辰动物能够会淹死，因今发展率不成能无穷增大，这一点需要写作时在假定一节具体诠释缘由
逻辑斯谛函数（英语：logistic function）是一种常见的S型函数，其函数图像称为逻辑斯谛曲线（英语：logistic curve）。简单的逻辑斯谛函数可用下式暗示：
f\text{(}x\text{)}=\frac{L}{1+e^{-k\left( x-x_0 \right)}}


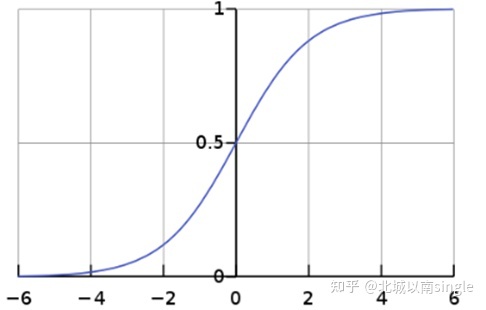
降水量为0时，假定发展率也为0，机关一个逻辑斯谛函数并减去降水量为0时的数值，就获得了降水量为0时发展率也为0的改良逻辑斯谛函数：（公式见文末）
其中Li为物种i的最大发展率，k 为逻辑斯谛增加率或曲线的陡度，h(t)为降水量。将上式代入式4，并把xi都写成t的函数
然后我们便可以自行机关天气条件（降水量），假定物种数目（比如3种 or 4种），设备相关参数，求解微分方程模子，画出各物种的数目变化曲线。然后就能停止各类分析




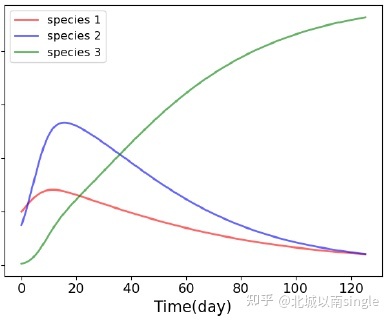
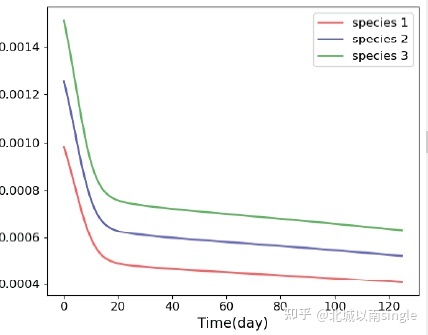
1.2就动物群落与大情况的持久相互感化，探讨你能从你的模子中得出什么结论。请斟酌以下题目。 • 社区需要几多种分歧的动物物种才能受益，随着物种数目的增加会发生什么？

社区需要几多种分歧的动物物种才能受益，这明显是个最优化题目，建立最优物种合作微分方程模子，
思考优化变量是什么：明显是动物物种的数目
思考方针函数是什么：长时候稳定状态下动物生物量的总和最大
什么是生物量，简单来说就是有机物的含量，有机物越多，说明这个群落就越强大，具体模子见文末
1.3社区中的物品种型若何影响你的成果？

这题可以和题目2一路建模和回答（建模时没有需要把这几个题目区分的这么明显，这点美赛和国赛分歧，你如果把每个题目都具体建模息争释，那底子没偶然候和精神），也就是在题目2中就间接引入物品种型这个身分。
物品种型：暂定为草本、灌木、树木这三种，草本、灌木、树木的生物量明显是逐步增加的，而种群数目（题目1中的xi）是逐步减小的，我们可以收集数据，肯定一棵草本、灌木、树木的生物量，比如一棵草的生物量是1，灌木为10，树木为100，对应物品种型的生物量乘以第一问的种群数目（题目1中的xi）就获得了总的生物量
优化变量：草本、灌木、树木别离有几多种
方针函数：长时候稳定状态下动物生物量的总和最大
优化模子方程形式：见文末文档，后续延续更新代码
1.4 在未来的天气周期中，干旱发生的频次更高、变化更大会发生什么影响?假如干旱不那末频仍，那末物种数目对整体种群的影响能否不异?

干旱发生的频次更高、变化更大会发生什么影响，翻译成人话：
频次更高：一段时候内设备降水量较少的时候段的数目
变化更大：降水量较少的时候段的延续时候，降水量削减的水平
1.5 净化和栖息地削减等其他身分若何影响你的结论？

1.6 你的模子表白，为确保一个动物群落的持久保存才能，应当做些什么，对大情况有什么影响？

按照前面几个题目标结论停止适当的语文建模，后续更新见文末地址
参考

• ^2023美赛A题 https://mbd.pub/o/bread/ZJWWkply
  

原文地址：https://zhuanlan.zhihu.com/p/607390737
免责声明：
1、文章部分图片源于收集，均为表示图；
2、一切文章、图片、音频视频文件等材料版权归版权一切人一切；
3、因非原创文章及图片等内容没法和版权者联系，如原作者或编辑以为作品不宜上网供阅读，或不应无偿利用，请实时告诉我们，以敏捷采纳适当办法，避免给双方形成不需要的经济损失；
4、本页面内容由爬虫法式自动收集于互联网，如无意中加害了媒体或小我的常识产权，请电邮【E-Mail:cb@yoyodoc.com】告之，我们将于24小时内删除。