给未来写信——时候胶囊技术

忆清静丫

来历：知乎



摘要

时候胶囊，意在信息被加密后，必须在特定的时候事后才能实现解密，而不管解密方或进犯者具有几多计较资本。
一、物理天下的时候胶囊

物理天下的时候胶囊，是指把物品封存在一个较小的空间（即称为“胶囊”），设定好未来开启的时候，只要到了预定的时候才能开启。一些设按时候比力久长的时候胶囊大多埋在地下或修建物地基中。这里，我们先容两个著名的时候胶囊。
1.1  纽约世博会时候胶囊
1938年9月23日，由美国西屋电气公司建造的“时候胶囊”被埋入了1939年纽约世博会举行地的地下，这个计划要到5000年后开启。它包括了物理学家爱因斯坦给5000年先人类的一封信《致先人书》。此外，在1964年纽约世博会，1970年日本大阪世博会上，也都埋下了时候胶囊。
1.2  乔布斯时候胶囊
1983年，在阿斯彭召开的一次设想者会议谢幕以后，会议构造者在当地埋藏了一个时候胶囊，官方称之为“Aspen Time Tube”。这个时候胶囊内的物品是由众多预会者配合捐献的，有魔方、姓名标签、穆迪·布鲁斯记录，甚至是啤酒等，可是由于前苹果CEO史蒂夫·乔布斯捐献了其在会议中展现的丽萨鼠标而终极以“乔布斯时候胶囊”命名[1]。乔布斯时候胶囊已按预按时候于埋藏30年后的2013年挖掘。
二、数字时候胶囊

前面先容的都是物理天下的时候胶囊。物理天下的时候胶囊靠物理的约束来“保证”翻开时候。胶囊中，也可以放置信函、书籍等内容。若何在数字天下实现时候胶囊，即给未来写信呢？物理的时候胶囊，在翻开之前，我们是看不到里面的情况的。数字天下的时候胶囊也应当实现“翻开”之前看不到其中的信息！这就要求在“到期”之前，接收方或任何其他的人没法解读出信息内容。从而实现“将信息发送到未来”的目标。这个概念最早由May于1993年在一个邮件列表中公然提出[2]，May将其称为“随时候开释的密码”--Timed-Release Crypto。
究竟上，有一些简单的方式可以实现“将信息发送到未来”的目标，例如，经过把密钥托管给可信第三方，在指定的时候由第三方将密钥供给给信息接收方即可。这类依靠第三方托管密钥的方式固然有其不敷，由于托管方能够作恶，提早向信息接收者供给密钥大概公布密钥。本文将先容，若何经过技术手段，实现除信息发送方外的其他任何人没法提早于指按时候从密文解密出明文信息。我们也可以将这一技术称为随时候开释的密码或延时揭秘（timed-release crypt）、时候胶囊（Time Capsule）、时候锁定加密（Time-lock encryption）等。
三、基于hash迭代的时候胶囊

本章会商可具体实现的时候胶囊算法。
3.1  根基思惟
要到达解密方不能提早解密，可以经过大量的计较来“消耗”解密方的时候，而且要使得即使是具有大量计较资本的解密方也不成能提早解密出明文信息。固然，计较劲的设想也要适中，假如只要具有超级计较才能的人材能解密，则算法也不具有现实利用代价。
要做到具有大量计较资本的人不具有明显上风，则算法应消除并行计较的上风,即设想为串行计较方式。这将使得任何人的计较都遭到当前计较芯片才能的限制，而没法提早解密出信息。用Rivest[3]的话说就是一个妇女需要怀孕9个月才能生一个健康的宝宝，我们不能让两个妇女怀孕4.5月就生一个健康的宝宝。



  图1 两个妇女怀孕4.5月也不能生出一个健康宝宝

（图片来自[3]）
一个方式是间接设想一个串行的算法，而更好的方式是以一个串行的方式为根本，停止多轮的迭代，在上一轮没有完成前，没法开启下一轮，从而强迫实现轮与轮之间的串行。多轮迭代的方式还有一个益处是，迭代轮数的调剂恰好对应所需时候的调剂，很是灵活。
3.2  一个直观的处理方式
我们都晓得，为了消除并行上风，就必须得采用串行大概迭代的方式，而hash函数的迭代运算恰好满足这一要求[4]。假定，有消息m,我们选一个随机数r，然后对r做T次hash迭代，获得k：



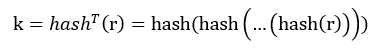
（公式1）

然后以k作为加密密钥，抵消息m停止加密，即：
c=E_k (m)  （公式2）
获得密文c，这里的加密算法可所以任何平安的对称密码算法（注：固然，用非对称密码算法也是可以的，只是这时辰k的计较需要与解密密钥相关，感爱好的读者可以自行设想。），如国密算法的SM4、SM7等。然后把k烧毁，并把（c,r,T）发送给接收方。则接收方由r和T经过（公式1）计较出k，然后以k为密钥解密密文c，即：
m=D_k (c) （公式3）
从而获得明文m。（注：究竟上，假如k的长度即是消息m的长度，则加解密算法也可以间接用异或运算来取代，行将明文或密文与k异或即得密文或明文，假如k的长度大于m的长度，截取其与m等长的部分亦可。）
这里，T的巨细可以按照需要调剂，当T越大，则解密需要的时候就越长。
固然，对于一样的hash函数运算，在分歧的软硬件上，其所需时候是纷歧样的。我们假定针对某个特定的hash函数，比如国密算法SM3，当前最快最高效的软硬件连系，在1秒内可以运转x次SM3运算，而我们需要设定的提早时候为y（单元以秒计），因而设定T=x*y。则任何人不能以低于y的时候解密出明文，从而到达预定目标。
3.3  分析
上述方式看起来没有什么题目，但是，加密与解密信息所需的计较是相当的。解密需要几多计较劲，加密也需要几近同等的计较劲。如图2所示，加密解密相当于在一个双向车道的门路上由一端到那一端，所经过的途径是等长的。



图2 加密息争密计较劲相当

这在某些提早时候不需要太长的利用中是可以接管的，如投标，凡是只需要期待几小时大概几天开标。可是，对于那些要求提早时候较长的利用，如遗言之类，是分歧适的，由于没有人愿意花费数年或数十年的时候去加密一个遗言。
四、 基于时候锁谜题的时候胶囊

上述基于hash迭代的时候胶囊，假如发送方希望接收方花多长时候解密，则自己也必须花多长时候来加密，这在现实利用中明显分歧适。
Rivest等人[4]提出了利用“时候锁谜题”来实现时候胶囊的方式。假定消息发送方有待发送的明文消息m，其可以停止以下操纵：
（1）类似于公钥密码算法RSA中的密钥天生方式，挑选大素数p和q，计较n=p*q；
（2）计较:
a_0=2 mod(n)  （公式4）



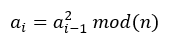
（公式5）

将（公式5）迭代计较T次（这里假定计较T次所需时候就是预设时候，T的巨细可按照需要调剂）即得：



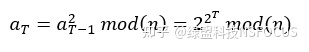
（公式6）

（3）计较消息密文为明文与上述成果的异或：
c=m XOR a_T   （公式7）
（4）消息发送方将(n,T，c)发送给接收方，并烧毁p,q和aT。
接收方收到(n,T，c)今后，依照公式（4）-（6）计较出aT，然后便可以计较密文c与aT的异或，即得明文：
m=c XOR a_T （公式8）
按此方式，接收方计较aT的时候与T成反比，且只能是串行计较。
到这里，我们发现，消息发送方和接收方的计较劲几近是一样的，这与前面的hash迭代运算又有什么区分呢？究竟上，由于发送方有关于p和q的信息，其不用照（公式5）那样计较T次，其有更加速速的方式计较出aT。设
∅=(p-1)(q-1) （公式9）
我们晓得，由欧拉定理，有：



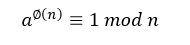
（公式10）

其中，a为任何不即是p和q且小于n的正整数。
因而，消息发送方仅需经过以下2步计较，便可快速获得aT：(2)* 计较：
b=2^T  mod ∅(n)  （公式11）
a_T=2^b  mod n （公式12）
注：（公式11）和（公式12）的关系建立，是由于由（公式11）可知存在某个x使得下式建立：
2^T=x*∅(n)+b （公式13）
因而



（公式14）

由上述分析可知，发送方把握了p和q的信息，其可以很轻易的走“捷径”计较出密文，形象地暗示如图3所示。而接收方，必须依照（公式5）循序渐进地停止T次平方取模运算，形象地暗示如图4所示，T的巨细决议了接收方解密所需时候的是非。



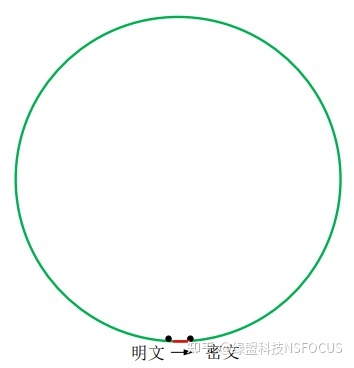
图3  发送方加密走“捷径”，所需计较劲小



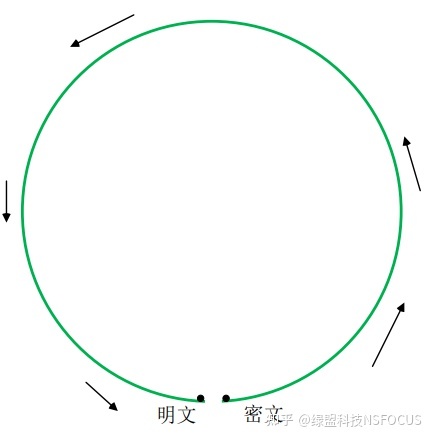
图4  接收方无捷径可走，所需计较劲大

是以，基于时候锁谜题的时候胶囊可以实现：1. 加密所需时候很短；2.解密所需时候（对应的计较劲）由加密时设定。其较好的满足了时候胶囊的根基要求。
五、时候胶囊利用

时候胶囊有很多的利用处景，这里罗列部分。
（1）遗言
例如，某人能够会提早立下遗言，而不愿意过早地表露其遗言内容，担忧会引发胶葛。



图5  遗言托管 （图片来自收集）

（2）投标
凡是情况下，投标要求，一是必须在指按时候条件交投标，二是必须在指按时候后才公布投标内容。这中心会有一个时候差。现场投标可以经过物理检查的方式实现上述要求。可是电子投标的情况下，假如没有合适的平安办法，也许你的投标，会被人提早翻开而泄露给你的合作对手。经过时代胶囊，可以实现除加密者自己外没有人可以提早翻开投标信息（如报价）。
（3）电子投票/选举
与投标类似，凡是要求在特定的时候之前投出选票，可是不希望任何人在唱票之前得悉投票的内容。



图6  投票 （图片来自收集）

其他利用还有抵押提早付出、密钥托管等等。
除上述利用外，时候胶囊的思惟还可以用于其他的一些密码学范畴，如连系不经意传输（oblivious transfer）协议进步不经意传输的灵活性[5]。时候锁谜题也可以用于机关可考证提早函数VDF，这是一种在区块链、博彩等范畴具有普遍利用的提早函数[6]。
六、时候胶囊的进一步成长

6.1  存在的题目
上述时候锁定计划简单易懂易实现，合适非专业人士了解，却也还存在适用性差等一些题目，例如：
（1）不能匿名（如无记名投票需要匿名性）；
（2）解密需要大量的计较；
（3）接收方需要实时启动计较，否则不能在预按时候完成解密；
（4）设想时难以较为正确地估量对手的计较才能，特别是未来的计较才能。
关于提早时候的设想，对于较为短期的，可以较为切确，对于时候较长的设想，由于对技术成长的猜测能够与现实的发生之间存在误差，则现实解密的时候能够与设想存在差别。例如，1999年，Rivest [7-8]给出了一个公然的时候锁加密应战，其最初设想的方针是使得该应战要经过35年才能被解密。而在应战公然恰好20年后即2019被破解，其中一个破解者（小我）从2016年头起头，采用基于软件的方式，花了3年零三个月的时候，另一组破解者（团队）则经过FPGA的方式，花了2个月的时候破解。Rivest认可，在设想之初，未斟酌到FPGA成长如此之快。2019年，Rivest又给出了一个新的应战[8],感爱好的可以尝试破解。
针对上述弱点，学术界提出了一些新的更先辈更适用的方式，如采用基于时候办事器的方式[10]、基于身份的方式[11]等。感爱好的读者可以进一步阅读相关文献。
6.2  连系存证更具利用潜力
前面讲到的投标和遗言等题目，都需要有响应的时候证实，比如，要求在某个时候点之条件交标书。而对于遗言，由于立遗言的人能够会点窜遗言，当出现两份纷歧致的遗言时，需要以最新的遗言为准。这些都需要供给时候证实。是以，时候胶囊与存在性证实相连系是必定的。区块链天生就是个杰出的无中心/无需可信第三方的存证平台，连系区块链的时候胶囊一定更具利用潜力，学界也提出了一些算法，例如[12-15]，倡议进一步阅读。
参考文献
[1] “乔布斯时候胶囊“，百度百科，拜候时候：2021.08
[2] May, T.C.: Timed-release crypto (1993), http://cypherpunks.venona.com/date/ 1993/ 02/ msg00129.html. 拜候时候：2021.08
[3] Rivest, R.L. LCS35 Time Lock Crypto Puzzle.，https://people.csail.mit.edu/rivest /pubs/ Riv19f.ppt 。拜候时候：2021.08
[4] Rivest, R.L., Shamir, A.,Wagner, D.A.: Time-lock puzzles and timed-release crypto. Massachusetts Institute of Technology (1996).
[5] Ma Xu, Xu Lingling, Zhang Fangguo. Oblivious transfer with timed-release receiver's privacy. Joumal of Systems and Software， 2011, 84(3): 460-464.
[6] Krzysztof Pietrzak, Simple Verifiable Delay Functions, https://eprint.iacr.org/2018/627.pdf.
[7] https://people.csail.mit.edu/rivest/lcs35-puzzle-description.txt, 拜候时候：2021.08
[8] Lcs35 https://github.com/supranational/lcs35， 拜候时候：2021.08
[9] Rivest, R.L., Description of the CSAIL2019 Time Capsule Crypto-Puzzle， https://people.csail.mit.edu/rivest/pubs/Riv19f.new-puzzle.pdf，  拜候时候：2021.08
[10] Ian F. Blake and Aldar C-F. Chan， Scalable, Server-Passive, User-Anonymous Timed Release Public Key Encryption from Bilinear Pairing， https://eprint.iacr.org/2004/211，拜候时候：2021.08
[11] Aldar C.F. Chan，Ian F. Blake, Scalable, Server-Passive, User-Anonymous Timed Release Cryptography, DOI：10.1109/ICDCS.2005.72
[12] Chae, S.W., Kim, J.I., Park, Y.: Practical time-release blockchain. Electronics 9(4) (2020)
[13] Jie Xiong and Qi Wang, Anonymous Auction Protocol Based On Time-released Encryption Atop Consortium Blockchain, IJAIT. Vol. 9, No.1, 2019.
[14] Wei-Jr Lai, Chih-Wen Hsueh, Ja-Ling Wu, A Fully Decentralized Time-Lock Encryption System on Blockchain, 2019 IEEE International Conference on Blockchain, DOI 10.1109/Blockchain.2019.00047
[15] Lijiao Chen, Kewei Lv and Dequan Li, Attack on Practical Time-Release Blockchain, to be published.




原文地址：https://zhuanlan.zhihu.com/p/407833441
免责声明：
1、文章部分图片源于收集，均为表示图；
2、一切文章、图片、音频视频文件等材料版权归版权一切人一切；
3、因非原创文章及图片等内容没法和版权者联系，如原作者或编辑以为作品不宜上网供阅读，或不应无偿利用，请实时告诉我们，以敏捷采纳适当办法，避免给双方形成不需要的经济损失；
4、本页面内容由爬虫法式自动收集于互联网，如无意中加害了媒体或小我的常识产权，请电邮【E-Mail:cb@yoyodoc.com】告之，我们将于24小时内删除。